MAA11 Algoritmit ja lukuteoria
Monte Carlo -simulaatioita
Monte Carlo -simulaatioiden ajatuksena on arvioida jonkin suureen arvoa hyödyntämällä satunnaislukuja. Menetelmä on saanut nimensä Monacossa sijaitsevan Monte Carlon kasinoista.Klassinen esimerkki Monte Carlo -simulaatiosta olisi arvioida luvun π arvoa arpomalla satunnaislukuja x ja y väliltä [–1,1] ja katsoa, kuinka suuri osa pisteistä (x,y) osuu origokeskisen yksikköympyrän sisään. Jos x2+y2 ≤ 1, piste osuu ympyrän kehälle tai sisälle, ja jos x2+y2 > 1, piste on ympyrän ulkopuolella.
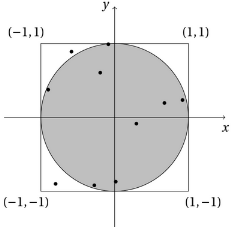
Toisaalta tasaisesti jakautuneista satunnaisluvuista tiedetään, että todennäköisyys osua tietylle alueelle on verrannollinen alueen pinta-alaan. Yksikköympyrän pinta ala on π·12 = π ja sitä ympäröivän neliön pinta-ala on 2·2 = 4. Yksittäisen pisteen (x,y) todennäköisyys osua ympyrän sisään on siis π/4.
Kun arvotaan n pistettä (x,y), joista k osuu ympyrän sisään, pätee suurten lukujen lain mukaan k/n ≈ π/4 ja likiarvo on todennäköisesti sitä parempi, mitä suurempi n on. Luvun π likiarvoksi saadaan siis suurilla luvun n arvoilla π ≈ 4·k/n.
Esimerkiksi seuraavassa kuvassa n = 10000, k = 7848 ja π ≈ 4·7848/10000 ≈ 3,139.

Käytetty koodi näytti tältä:
import random
osumat = 0
n = 10000
for i in range(n):
x = random.uniform(-1,1)
y = random.uniform(-1,1)
if x**2 + y**2 <= 1:
osumat += 1
print(osumat)
print(4*osumat/n) # pii
Monte Carlo -menetelmien käyttö
Todettakoon, että edellä esitetty menetelmä luvun π likiarvon laskemiselle on hyvin tehoton, mutta toisaalta yksinkertainen toteuttaa. Laskennallisen raskautensa vuoksi Monte Carlo -menetelmiä käytetäänkin yleensä tilanteissa, joissa hienostuneemmat menetelmät pettävät.Esimerkiksi monimutkainen satunnaisuutta sisältävä fysiikkasimulaatio voidaan ajaa monta kertaa ja lopputulosten todennäköisyysjakaumaa arvioida Monte Carlo -jakauman perusteella. Kuvien renderöiminen path tracing -tekniikoilla on toinen esimerkki Monte Carlo -sovelluksesta: kun riittävän monen valonsäteen osin satunnaista heijastumista ja taittumista 3D-mallissa seurataan joko valonlähteestä kameraan tai kamerasta valonlähteeseen, voidaan niiden tuottaman valon keskiarvona saada realistisen näköinen kuva. Hyvän laadun saaminen vaatii pitkän laskenta-ajan.

Path tracing -tekniikalla tuotettu kuva (lähde, laatija nimimerkki Qutorial, CC-BY-SA 4.0 -lisenssi)
Tehtävä 1 Ratkaisematon
Tasojoukon A pisteet (x,y) määräytyvät epäyhtälöistä 0 ≤ x ≤ 2, 0 ≤ y ≤ 4 ja y ≥ x2. Tässä tehtävässä on tarkoitus arvioida joukon A pinta-alaa simulaation avulla käyttämällä sitä tietoa, että todennäköisyys on suoraan verrannollinen pinta-alaan. Arvotaan pisteitä (x,y) suorakulmiosta B, jonka määräävät epäyhtälöt 0 ≤ x ≤ 2 ja 0 ≤ y ≤ 4.
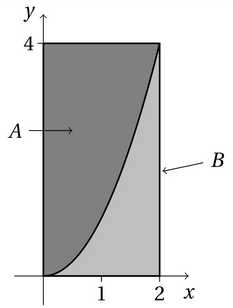
Tee koodi, joka arpoo 1000 pistettä suorakulmiosta B. Ohjelman tulee tulostaa peräkkäisille riveille
- niiden pisteiden lukumäärä, jotka kuuluvat joukkoon A
- tämän perusteella laskettu likiarvo alueen A pinta-alalle.
Vihje: Komennolla import random
saat käyttöön kirjaston random, jonka komennolla
random.uniform(a,b)
saat pseudosatunnaisen reaaliluvun väliltä [a,b].
Kirjoita ohjelma tähän:
Tehtävä 2 Ratkaisematon
Heitetään noppaa, kunnes saatujen silmälukujen summa on 20 tai suurempi. Tehtäväsi on laskea odotusarvo heittojen määrälle.Toteuta tämä tekemällä 1000 kertaa simulaatio nopan heittämisestä ja laskemalla heittomäärien keskiarvo. Kyseessä on tavallinen noppa, eli silmäluvut ovat 1–6.
Vihje: Satunnaisen kokonaisluvun väliltä [a,b] saa
random-kirjaston komennolla random.randint(a,b).
Kirjoita ohjelma tähän: