Tie koodariksi

Kirjaudu sisään

MAA11 Algoritmit ja lukuteoria

★
Kieli:

Yhtälön numeerinen ratkaiseminen

Oppimateriaalit peruskoulussa ja lukiossa vilisevät yhtälöitä, jotka on mahdollista ratkaista tarkasti. Monet käytännön ongelmiin liittyvät yhtälöt eivät kuitenkaan ole ratkaistavissa muuten kuin likimääräisesti. Tällöin astutaan numeerisen matematiikan pariin. Numeriikka on matematiikan haara, joka käsittelee likiarvoilla laskevia algoritmeja.

Nykyään numeerinen laskenta tehdään luonnollisesti tietokoneella. Oleellista on tuloksen tarkkuuden lisäksi laskentaan kuluva aika. Vaikkapa tietokonepeleissä näytön tulisi päivittyä lukuisia kertoja sekunnissa, jolloin pikselien oikeat värit täytyy laskea nopeasti. Myöskään sään ennustamisessa ei ole mieltä, jos huomisen ennuste on valmis vasta ensi viikolla.

Nasan simulaatio hurrikaaneista vuodelta 2012. Vapaa ei-kaupallinen käyttö (Wikimedia Commons)

Brute Force

Ratkaistaan yhtälö $4x^4-x^3-5x^2+1=0$. Yhtäpitävästi voidaan ratkaista funktion $f(x)=4x^4-x^3-5x^2+1$ nollakohdat.

Yksinkertaisin tapa ratkaisuun on laskea suuri määrä funktion arvoja ja katsoa, missä kohtaa funktion arvo vaihtaa merkkiä. Tämä vastaa oleellisesti ottaen funktion kuvaajan piirtämistä tietokoneella.

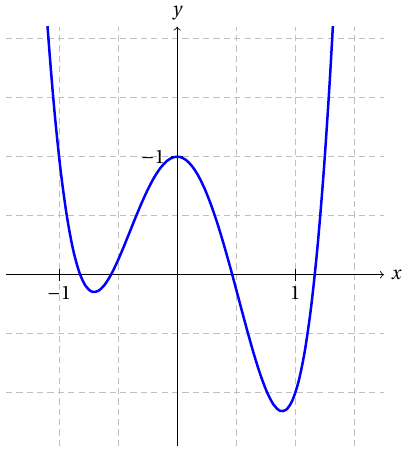
Menetelmää voisi kutsua leikkisästi brute force -menetelmäksi, koska laskenta-aika on huomattavan suuri saavutettavaan tarkkuuteen nähden.

Esimerkki

Python-koodina laskennan voisi toteuttaa seuraavasti. Neljäs desimaali voi olla väärin pyöristyksessä syntyvän virheen vuoksi. 
def f(x):
    return 4*x**4 - x**3 - 5*x**2 + 1

print("Tulostetaan funktion nollakohtien likiarvot:")

x = -2                  # Alkuarvo
askelpituus = 0.0001
ylaraja = 2             # Mihin laskenta lopetetaan

f1 = f(x)

while x < ylaraja:
    x = x + askelpituus
    f2 = f(x)
    if f1*f2 < 0 or f2 == 0:
        print(round(x,4))
    f1 = f2
Tuloste: 
Tulostetaan funktion nollakohtien likiarvot:
-0.8208
-0.5605
0.4665
1.165

Puolitushaku

Puolitushaku löytää jatkuvan funktion nollakohdan kahden erimerkkisen arvon välistä. Jos esimerkiksi $f$ on jatkuva funktio, $a < b$, ja arvoilla $f(a)$ ja $f(b)$ on eri merkki, Bolzanon lauseen nojalla välillä $]a, b[$ on funktion nollakohta.

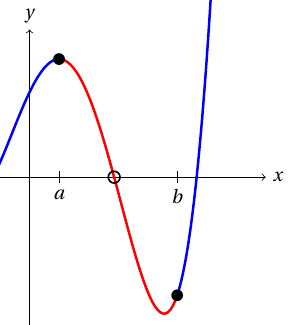
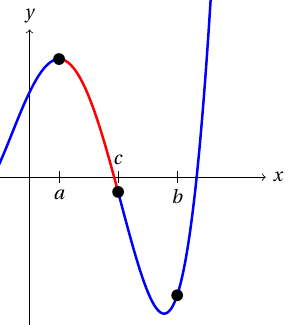
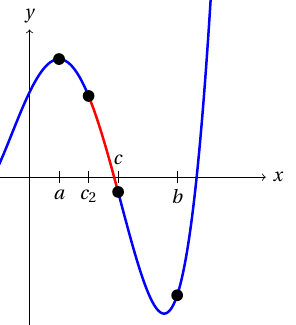
Puolitushaussa tarkastellaan funktion merkkiä välin keskipisteen $c =\dfrac{a+b}{2}$ kohdalla. Jos $f(c) = 0$, nollakohta on löytynyt. Jos taas $f(c) \neq 0$, joko luvuilla $f(a)$ ja $f(c)$ tai luvuilla $f(b)$ ja $f(c)$ on eri merkki. Näin voidaan siirtyä tarkatelemaan puolitettua väliä $]a, c[$ tai $]c, b[$.

Tätä toistetaan, kunnes välin pituus $x$-akselilla on pienempi kuin tavoiteltu tarkkuus.

Tehtävä 1 Ratkaisematon

Kirjoita ohjelma, joka ratkaisee funktion $f(x) = x^5 + x^3 - 7$ ainoan nollakohdan puolitushaulla käyttäen alkuarvoja $x = 1$ ja $x = 2$. Likiarvon virhe tulee olla pienempää kuin $10^{-6}$.

Automaattista tarkistusta varten ohjelman tulee tulostaa jokaisen tutkitun välin keskipiste. Tulostuksen tulisi alkaa 

1.5
1.25
ja päättyä riittävän tarkkaan likiarvoon nollakohdalle.

Kirjoita ohjelma tähän:

Newtonin menetelmä

Newtonin menetelmä funktion nollakohdan ratkaisemiseksi perustuu siihen, että derivoituva funktio on pienessä mittakaavassa likimain lineaarinen. Funktion nollakohdan likiarvoksi kelpaa siis funktion tangenttisuoran nollakohta, joka on helpompi laskea.

Newtonin menetelmässä lähdetään liikkeella alkuarvauksesta $x_0$. Tässä kohdassa funktion $f$ arvo on $f(x_0)$ ja tangentin kulmakerroin $f'(x_0)$. Jos tangentin nollakohta on $x_1$, pätee \[ f'(x_0) = \dfrac{f(x_0)-0}{x_0-x_1}, \] josta ratkaistuna \[ x_1 = x_0-\dfrac{f(x_0)}{f'(x_0)}. \]

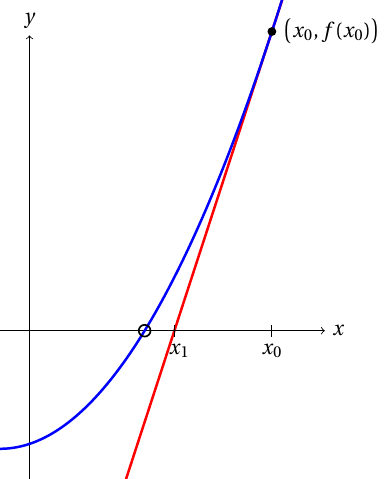
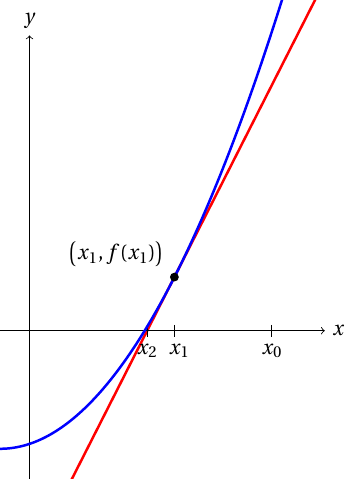
Prosessi voidaan aloittaa alusta pisteestä $x=x_1$, jolloin saadan jono $x_0$, $x_1$, $x_2$... yhä tarkempia likiarvoja nollakohdalle. Yleinen iterointikaava on \[ x_{n+1} = x_n-\dfrac{f(x_n)}{f'(x_n)}. \] Iteroiminen eli toistaminen voidaan lopettaa, kun peräkkäisten muuttujan $x$ arvojen erotus, eli $\dfrac{f(x_n)}{f'(x_n)}$, on riittävän pieni.

Newtonin menetelmä on erittäin nopea silloin kun se toimii. Valitettavasti iteraatio ei kuitenkaan aina suppene. Esimerkiksi derivaatan nollakohtaan osuminen aiheuttaa nollalla jaon, ja toisinaan suppeneminen riippuu sopivan alkuarvon valinnasta.

Tehtävä 2 Ratkaisematon

Kirjoita ohjelma, joka etsii funktion $f(x) = x^5 + x^3 - 7$ ainoan nollakohdan Newtonin menetelmällä käyttäen alkuarvoa $x_0 = 1.5$. Tulos saa poiketa oikeasta tuloksesta korkeintaan $10^{-6}$.

Automaattista tarkistusta varten ohjelman tulee tulostaa alkuarvo ja jokaisen iteraatiokierroksen tulos omille riveilleen. Tulostuksen pitäisi siis alkaa (ainakin likimain) 

1.5
1.3762183235867447
ja viimeisellä rivillä tulisi olla riittävän tarkka likiarvo.

Kirjoita ohjelma tähän:

Esimerkki

Newtonin menetelmällä voi ratkaista tehokkaasti likiarvoja esimerkiksi neliöjuurille. Luku $\sqrt{2}$ on nimittäin funktion $f(x)=x^2 - 2$ nollakohta. Derivaataksi saadaan $f'(x)=2x$, joten iterointikaava on \[ x_{n+1} = x_n-\dfrac{f(x_n)}{f'(x_n)}= x_n-\dfrac{x_n^2-2}{2x_n}. \] Tämän voi vielä sieventää muotoon \[ x_{n+1} = \frac12x_n+\frac{1}{x_n}. \] Vaikkapa alkuarvolla $x_0 = 1$ saadaan \begin{align*} x_1 &= \frac12x_0+\frac{1}{x_0} = \frac12\cdot 1 +1 = 1.5 \\ x_2 &= \frac12x_1+\frac{1}{x_2} = \frac12\cdot 1.5 +\frac{1}{1.5} = 1.41666... \\ x_3 &= 1.414215686274509...\\ x_4 &= 1.414213562374689...\\ x_5 &= 1.414213562373095... \end{align*} Luvussa $x_5$ kaikki esiin kirjoitetut desimaalit ovat jo oikein.

Tehtävä 3 Ratkaisematon

Kirjoita Newtonin menetelmään perustuva algoritmi, joka laskee luvun $\sqrt[3]{2}$ likiarvon. Virhe saa olla korkeintaan $10^{-9}$. Kuten aiemmassa esimerkissä, algoritmi saa käyttää vain yhteen-, vähennys-, kerto- ja jakolaskua.

Ohjelman tulee tulostaa vain vastaus.

Kirjoita ohjelma tähän: