MAA11 Algoritmer och talteori

Delbarhet och primtal

Euklides algoritm

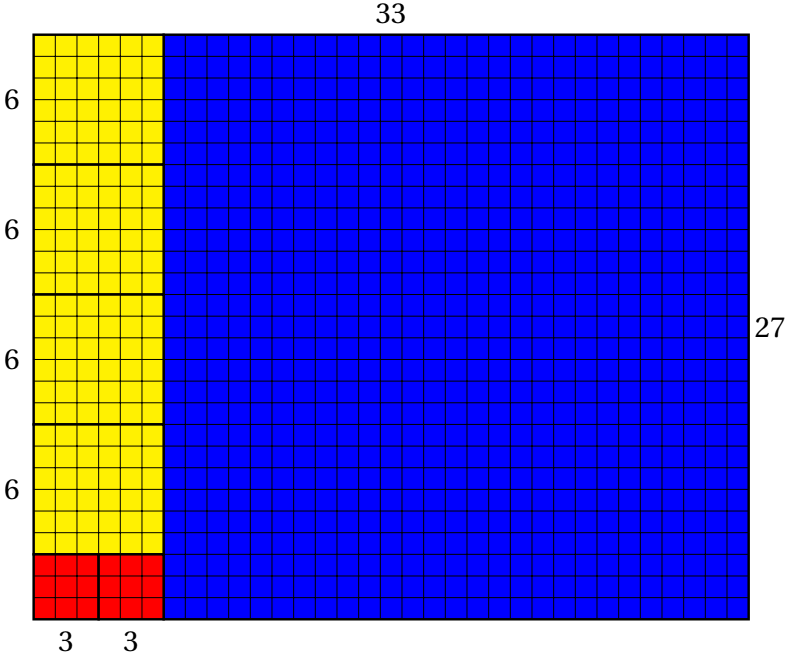
Euklides algoritm bestämmer den största gemensamma delaren till två positiva heltal. Algoritmen baseras på ett resultat, enligt vilket de gemensamma delarna i talen $a$ och $b$ i ekvationen \[a = qb + r\] är samma som de gemensamma delarna i talen $b$ och $r$. Division av talen $b$ och $r$ ger allt mindre tal, och svaret är klart när divisionen går jämnt ut. Till exempel \[\textrm{syt}(33, 27) = \textrm{syt}(27, 6)=\textrm{syt}(6, 3) = 3, \] eftersom $33 = 1\cdot 27 + 6 $, $27 = 4\cdot 6 + 3$ och $6 = 2\cdot 3 + 0$.

Den sista divisorn $3$ är den största gemensamma delaren. Processen kan åskådliggöras även på följande sätt:

---

Uppgift 1 Olöst

Skriv ett program, som beräknar den största gemensamma delaren för talen 210 592 578 och 120 065 279. Det är mest praktiskt att beräkna resten med operatorn %. Programmet ska enbart skriva ut svaret.

Skriv ditt program här:

---

Primtalstest

Ett primtal är ett heltal som är större än $1$ och som endast kan delas med sig självt och talet $1$. Med till exempel följande funktion kan man testa om det är fråga om ett primtal. Idén med algoritmen är att testa delbarheten hos talet $n$ genom att försöka dela det turvis med alla tal $2$, $3$, ... $n-1$. Denna algoritm är mycket långsam.

def ar_primtal(tal):
    if tal < 2:
        return False

    for divisor in range(2, tal):
        if tal % divisor == 0:
            return False

    return True

print(ar_primtal(137))

Utskrift:

True

Snabbheten hos algoritmen ovan kan testas genom att använda funktionen time i modulen time. Ett tillräckligt stort primtal väljs och testas:

from time import time

def ar_primtal(tal):
    if tal < 2:
        return False
    
    for divisor in range(2, tal):
        if tal % divisor == 0:
            return False

    return True

n = 30000001
starttid = time()
print(ar_primtal(n))
sluttid = time()

print("Tid i sekunder:")
print(sluttid-starttid)

Detta program har lång exekveringstid.

---

Uppgift 2 Olöst

Algoritmen i det föregående exemplet kan förbättras relativt enkelt. Om talet har delare, förekommer de i par: Till exempel \[36 = 2\cdot 18= 3\cdot 12 = 4\cdot 9 = 6\cdot 6.\] Om två delare är lika stora, är de kvadratrötter av det aktuella talet ($\sqrt{36}=6$). I övriga fall är den ena delaren mindre än kvadratroten och den andra är större.

Detta betyder att om talet $n$ inte är ett primtal, har det en delare som är större än ett och vars storlek är högst $\sqrt{n}$. Vid primtalstestning räcker det alltså att kontrollera divisorerna $2$, $3$, ..., $\sqrt{n}$.

Kopiera koden i föregående exempel och förbättra funktionen ar_primtal på tidigare nämnda sätt. Lämna programmets utskrifter såsom de är i exemplet. Kvadratrotskommandot sqrt finns i math-modulen.

Skriv ditt program här:

---

Eratosthenes såll

Eratosthenes såll upprätthåller en bokföring över talen 2...n. Algoritmen går igenom talen från det minsta till det största. Vid varje tal i markerar algoritmen multiplerna av talet 2*i, 3*i, 4*i osv. med ett kryss. Krysset betyder att det aktuella talet inte är ett primtal, eftersom det kan delas med talet i. När algoritmen är färdig identifieras primtalen genom att de inte har något kryss.

Vi kan till exempel kontrollera hur Eratosthenes såll fungerar, när n är 100. Då söker algoritmen alla primtal, som finns mellan 2...100. Detta är algoritmens utgångsläge:

Algoritmen kryssar först för multiplerna för talet 2, dvs. 4, 6, 8, osv.:

Sedan kryssar algoritmen för multiplerna för talet 3, dvs. 6, 9, 12, osv.:

Algoritmen fortsätter vidare på motsvarande sätt tills den har gått igenom alla talen mellan 2...100. Då är bokföringens innehåll följande:

Detta innebär att primtalen mellan 2...100 är:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Genomförande av sållet

För att vi ska kunna programmera Eratosthenes såll behöver vi ett sätt att komma ihåg bokföringen av talen. Ett bra sätt är att skapa en lista med plats för varje tal i bokföringen. Vi kan skapa listan på följande sätt:

sall = [0]*(n+1)

Punkterna i listan är numrerade 0, 1, 2, ..., n, och varje punkt börjar med talet 0. Idén är att i punkt sall[x] finns information om talet x har kryssats för. Värdet 0 betyder att talet inte har kryssats för, och värdet 1 betyder att talet har kryssats för. Observera att vi inte använder punkterna 0 och 1 ur listan i algoritmen, eftersom vi behöver bokföring först från och med punkt 2.

Följande kod genomför Eratosthenes såll:

n = 100
sall = [0]*(n+1)
for i in range(2,n+1):
    for j in range(2*i,n+1,i):
        sall[j] = 1

Kodens yttre loop går igenom talen 2...n, och vid varje tal i markerar den kapslade loopen att talets multipler 2*i, 3*i, 4*i, osv., inte är primtal.

Därefter kan vi skriva ut de identifierade primtalen så här:

for i in range(2,n+1):
    if sall[i] == 0:
        print(i)

Till exempel när n är 100, är kodens utskrift följande:

2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97

---

Uppgift 3 Olöst

Mellan 1...100 finns 25 primtal. Hur många primtal finns mellan 1...1 000?

Skriv ditt program här:

---

Uppgift 4 Olöst

Summan av primtalen mellan 1...100 är 1 060. Vad är summan av primtalen mellan 1...1 000?

Skriv ditt program här:

---

Uppgift 5 Olöst

Primtalspar bildas av två primtal, vars skillnad är 2. Mellan 1...100 finns följande primtalspar:

3 5
5 7
11 13
17 19
29 31
41 43
59 61
71 73

Gör ett program som skriver ut primtalsparen mellan 1...1 000 på motsvarande sätt.

Skriv ditt program här:

---