MAA11 Algoritmer och talteori

Språk:

Monte Carlo-metoder

Tanken med Monte Carlo-metoderna är att uppskatta värdet för en storhet genom att använda slumptal. Metoden har fått sitt namn efter casinot i Monte Carlo i Monaco.

Ett klassiskt exempel av en Monte Carlo-metod skulle vara att uppskatta värdet för talet π genom att lotta slumptalen x och y mellan [–1,1] och se hur stor andel punkter (x,y) som faller inuti enhetscirkeln med medelpunkten i origo. Om x²+y² ≤ 1, faller punkten på cirkelns omkrets eller inuti, och om x²+y² > 1, är punkten utanför cirkeln.

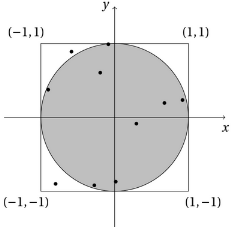
Å andra sidan vet man av jämnt fördelade slumptal att sannolikheten att falla på ett visst område är proportionellt med områdets area. Enhetscirkelns area är π·1² = π och den omkretsande kvadratens area är 2·2 = 4. Sannolikheten för en enskild punkt (x,y) att falla inuti cirkeln är alltså π/4.

När vi värderar n punkter (x,y), varav k faller inuti cirkeln, gäller enligt lagen om stora tal k/n ≈ π/4 och närmevärdet är sannolikt bättre ju större n är. Närmevärdet för talet π fås alltså med stora värden för talet n π ≈ 4·k/n.

Till exempel i följande bild n = 10000, k = 7848 och π ≈ 4·7848/10000 ≈ 3,139.

När den används ser koden ut så här:

import random

traffar = 0
n = 10000

for i in range(n):
    x = random.uniform(-1,1)
    y = random.uniform(-1,1)

    if x**2 + y**2 <= 1:
        traffar += 1

print(traffar)
print(4*traffar/n) # pi

Användning av Monte Carlo-metoder

Det bör noteras att den tidigare presenterade metoden för att beräkna närmevärdet för talet π är mycket ineffektiv, men å andra sidan är den enkel att utföra. På grund av sin beräkningsmässiga tunghet används Monte Carlo-metoderna vanligtvis i situationer där mer förfinade metoder sviker.

Till exempel kan en komplex fysiksimulering som innehåller slumpmässighet köras många gånger och slutresultatens sannolikhetsfördelning uppskattas utgående från Monte Carlo-fördelningen. Ett annat exempel på Monte Carlo-metoderna är att rendera bilder med path tracing-teknik: när tillräckligt många ljusstrålars delvis slumpmässiga reflektioner och brytning i en 3D-modell följs antingen från ljuskällan till kameran eller från kameras till ljuskällan, kan man som medeltal av det ljus de producerar få en realistisk bild. För att få en god kvalitet krävs lång beräkningstid.

Bild producerad med Path tracing-teknik (källa, gjord av pseudonymen Qutorial, CC-BY-SA 4.0-licens)

Uppgift 1 Olöst

Planmängden A:s punkter (x,y) bestäms av olikheterna 0 ≤ x ≤ 2, 0 ≤ y ≤ 4 och y ≥ x². I denna uppgift ska man bedöma arean hos mängden A med hjälp av simuleringen genom att använda informationen att sannolikheten är direkt proportionell mot arean. Vi genererar punkterna (x,y) ur rektangeln B, som bestäms av olikheterna 0 ≤ x ≤ 2 och 0 ≤ y ≤ 4.

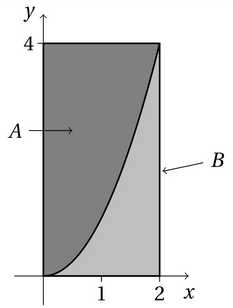
Gör en kod, som genererar 1000 punkter ur rektangeln B. Programmet ska på varandra följande rader skriva ut

antalet punkter, som tillhör mängden A
närmevärdet för arean av området A som beräknats utgående från dem.

[Uppgiften modifierats från uppgift 8 i studentskrivningarna våren 2021, lång]

Tips: Med kommandot import random får du tillgång till biblioteket random, med vars kommando random.uniform(a,b) du får ett pseudoslumpmässigt reellt tal mellan [a,b].

Skriv ditt program här:

Uppgift 2 Olöst

Vi kastar tärning tills summan av poängtalen är 20 eller större. Din uppgift är att beräkna väntevärdet för antalet kast.

Gör detta genom att göra en simulation av 1000 tärningskast och beräkna medelvärdet av antalet kast. Tärningen är en vanlig tärning med poängtalen 1–6.

Tips: Ett slumpmässigt heltal mellan [a,b] fås med random-bibliotekets kommando random.randint(a,b).