Tie koodariksi

Kirjaudu sisään

MAA11 Algoritmer och talteori

★
Språk:

Numerisk lösning av ekvationer

Studiematerialet i grundskolan och gymnasiet kryllar av ekvationer som är möjliga att lösa exakt. Många ekvationer som anknyter till praktiska problem kan emellertid inte lösas på annat sätt än ungefärligt. Då kommer numerisk matematik in i bilden. Numeriken är en gren av matematiken som behandlar algoritmer som räknas med närmevärden.

Numera görs numerisk beräkning med dator. Utöver resultatets noggrannhet är den tid som krävs för beräkningen viktig. Till exempel i dataspel där skärmen ska uppdateras otaliga gånger per sekund, varpå pixlarnas rätta färger snabbt ska beräknas. Det är heller ingen poäng med att förutspå vädret om morgondagens prognos är färdig först nästa vecka.

NASA:s simulation av orkaner från år 2012. Fri icke-kommersiell användning (Wikipedia Commons)

Brute Force

Vi löser ekvationen $4x^4-x^3-5x^2+1=0$. Samstämmigt kan vi lösa nollpunkterna i funktionen $f(x)=4x^4-x^3-5x^2+1$.

Den enklaste vägen till lösningen är att räkna en stor mängd av funktionens värden och se i vilket skede funktionens värde byter tecken. Detta motsvarar väsentligen att rita en funktionsgraf på datorn.

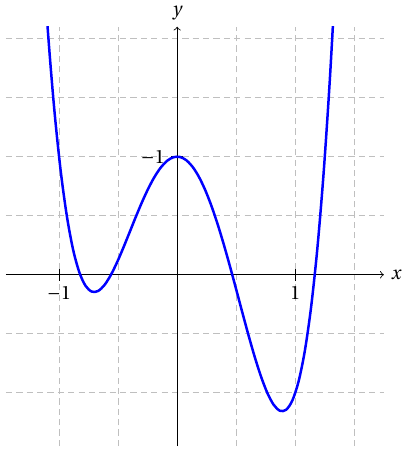
Metoden kan skämtsamt kallas brute force-metoden, eftersom beräkningstiden är mycket lång med tanke på exaktheten.

Exempel

Som Python-kod kunde beräkningen utföras på följande sätt. Den fjärde decimalen kan vara fel på grund av ett fel som uppstår vid avrundningen. 
def f(x):
    return 4*x**4 - x**3 - 5*x**2 + 1

print("Skriver ut närmevärdena av funktionens nollpunkter:")

x = -2 # Startvärde
steglangd = 0.0001
ovregrans = 2 # Var avslutas beräkningen

f1 = f(x)

while x < ovregrans:
    x = x + steglangd
    f2 = f(x)
    if f1*f2 < 0 or f2 == 0:
        print(round(x,4))
    f1 = f2
Utskrift: 
Skriver ut närmevärdena av funktionens nollpunkter:
-0.8208
-0.5605
0.4665
1.165

Halveringssökning

Halveringssökning hittar nollpunkten hos en kontinuerlig funktion mellan två värden med olika förtecken. Om till exempel $f$ är en kontinuerlig funktion, $a < b$, och värdena $f(a)$ och $f(b)$ har ett skilt tecken, med stöd av Bolzanos sats är $]a, b[$ funktionens nollpunkt.

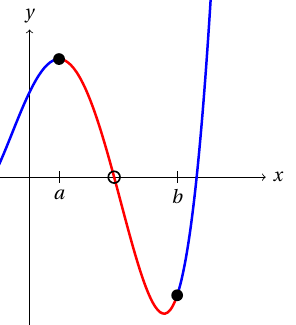
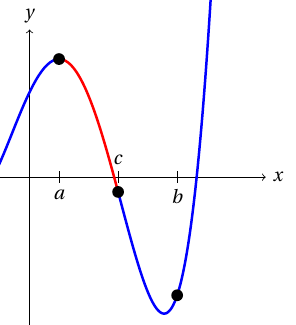
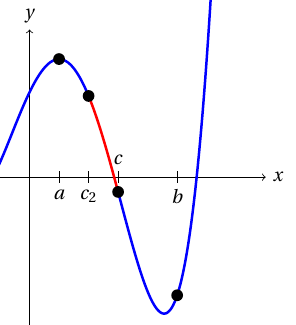
Vid halveringssökning kontrolleras funktionens tecken vid mittpunkten $c =\dfrac{a+b}{2}$. Om $f(c) = 0$ har nollpunkten hittats. Om däremot $f(c) \neq 0$ har antingen talen $f(a)$ och $f(c)$ eller talen $f(b)$ och $f(c)$ olika tecken. På så sätt kan man övergå till att kontrollera det halverade avståndet $]a, c[$ eller $]c, b[$.

Detta upprepas tills intervallens längd på $x$-axeln är mindre än den önskade exaktheten.

Uppgift 1 Olöst

Skriv ett program som löser den enda nollpunkten i funktionen $f(x) = x^5 + x^3 - 7$ med halveringssökning genom att använda startvärdena $x = 1$ och $x = 2$. Närmevärdets fel ska vara mindre än $10^{-6}$.

För automatisk granskning ska programmet mata ut mittpunkten på varje kontrollerad intervall. Utskriften ska börja 

1.5
1.25
och sluta tillräckligt exakt vid nollpunkten.

Skriv ditt program här:

Newtons metod

Newtons metod för att lösa nollpunkten i en funktion grundar sig på att den deriverande funktionen är i liten skala i det närmaste lineär. Som närmevärde för funktionens nollpunkt duger alltså nollpunkten för funktionens tangens, som är lättare att beräkna.

I Newtons metod börjar man med en inledande gissning $x_0$. I detta skede är värdet för funktionen $f$ $f(x_0)$ och tangensens vinkelkoefficient $f'(x_0)$. Om tangensens nollpunkt är $x_1$, gäller \[ f'(x_0) = \dfrac{f(x_0)-0}{x_0-x_1}, \] varav löst \[ x_1 = x_0-\dfrac{f(x_0)}{f'(x_0)}. \]

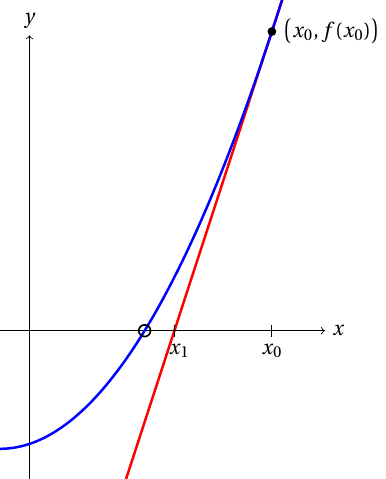
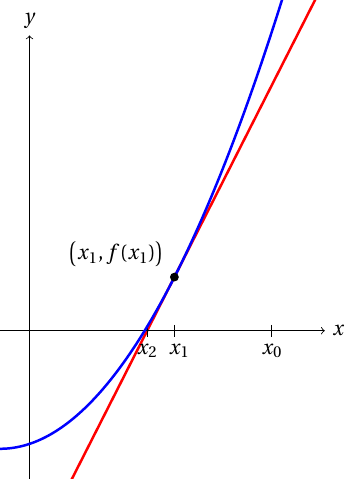
Processen kan börjas om från början från punkten $x=x_1$, varpå man får följden $x_0$, $x_1$, $x_2$... allt mer exakta närmevärden för nollpunkten. En allmän iterationsformel är \[ x_{n+1} = x_n-\dfrac{f(x_n)}{f'(x_n)}. \] Iterationen, dvs. upprepningen kan avslutas när skillnaden, dvs. $\dfrac{f(x_n)}{f'(x_n)}$, mellan de på varandra följande värdena för variabeln $x$ är tillräckligt liten.

Newtons metod är mycket snabb när den fungerar. Dessvärre konvergerar iterationen inte alltid. Till exempel orsakar träffande av derivatans nollpunkt division med noll, och å andra sidan beror minskningen på valet av ett lämpligt startvärde.

Uppgift 2 Olöst

Skriv ett program som söker den enda nollpunkten i funktionen $f(x) = x^5 + x^3 - 7$ med Newtons metod genom att använda startvärdet $x_0 = 1.5$. Resultatet får avvika från det korrekta resultatet med högst $10^{-6}$.

För automatisk granskning ska programmet mata ut startvärdet och resultatet för varje iterationsvarv på skilda rader. Resultatet ska alltså börja (åtminstone ungefär) 

1.5
1.3762183235867447
och på den sista raden ska stå ett tillräckligt exakt närmevärde.

Skriv ditt program här:

Exempel

Med Newtons metod kan man effektivt lösa närmevärden till exempel för kvadratrötter. Talet $\sqrt{2}$ är nämligen nollpunkt för funktionen $f(x)=x^2 - 2$. Derivatan blir $f'(x)=2x$, så iterationsformeln är \[ x_{n+1} = x_n-\dfrac{f(x_n)}{f'(x_n)}= x_n-\dfrac{x_n^2-2}{2x_n}. \] Denna kan ännu förenklas till \[ x_{n+1} = \frac12x_n+\frac{1}{x_n}. \] Med startvärdet $x_0 = 1$ får man \begin{align*} x_1 &= \frac12x_0+\frac{1}{x_0} = \frac12\cdot 1 +1 = 1.5 \\ x_2 &= \frac12x_1+\frac{1}{x_2} = \frac12\cdot 1.5 +\frac{1}{1.5} = 1.41666... \\ x_3 &= 1.414215686274509...\\ x_4 &= 1.414213562374689...\\ x_5 &= 1.414213562373095... \end{align*} I talet $x_5$ är alla utskrivna decimaler redan korrekta.

Uppgift 3 Olöst

Skriv en algoritm som baserar sig på Newtons metod som beräknar närmevärdet för talet $\sqrt[3]{2}$. Felet får vara högst $10^{-9}$. Såsom i tidigare exempel får algoritmen endast använda addition, subtraktion, multiplikation och division.

Programmet ska enbart skriva ut svaret.

Skriv ditt program här: